Recursion
The Recursive function is a function that calls itself to solve the problem.
When should we use recursion?
If any problem can be divided into multiple smaller version of the same problem, we can use Recursive approach to solve that problem.
Example
Calculate the factorial of a given number.
fact(3) = 6 (3 * 2 * 1)
This problem can be divided into three smaller versions.
Declare fact = 1
1. fact = fact * 3
2. fact = fact * 2
1. fact = fact * 1
Basic Rules of Recursion
1. The recursive function should call itself.
2. The recursive function should have an ending point where it doesn't make further recursive calls. Also called as the base case. Base case will not need any recursive call to solve.
Example Base cases
Factorial of 0 is 1 and 1 is 1.
Fibonacci of 0 is 0 and 1 is 1.
The above cases are straightforward and those cases don't need any recursive call.
3. All the recursive calls should align towards the base case.
Example
When calculating factorial(5). Here, base case is factorial(0) = 1 || factorial(1) = 1.
Recursive functions should go like factorial(5), factorial(4),factorial(3),factorial(2), finally ends with factorial(1) or factorial(0).
If it goes in another way like factorial(6)....factorial(100) etc. The recursion won't end.
Let's solve the factorial problem using recursion
Algorithm
1. Find the base case. factorial(0) = 1 || factorial(1) = 1.
2. Write the factorial function and call itself recursively untill it meets the base case.
3. Calculate and return the answer.
int factorial(int n) { //base case fact(0) = fact(1) = 1 if(n <= 1) return 1; //calculate the factorial //recursively the call the above function return n * factorial(n - 1); }
Visualizing the above recursive function
The best way of understanding the recursion is by visualizing it.
Let's understand how factorial(3) works.
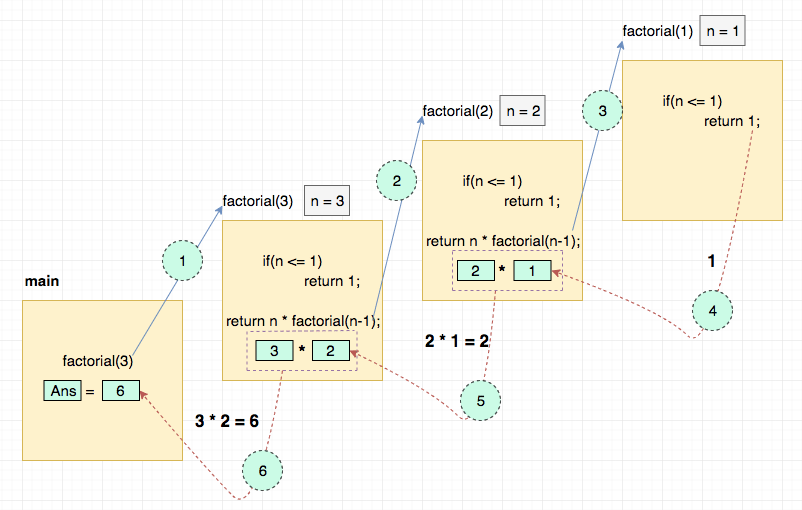
Factorial using Recursion
#include<stdio.h> int fact(int n) { if(n <= 1) return 1; return n * fact(n-1); } int main() { int n; scanf("%d",&n); if(n >= 0) printf("%d\n",fact(n)); return 0; }
Stack Overflow in Recursion
In recursion, the new function call will be created in stack memory section.
If our recursive function doesn't have any base case or the recursive function call doesn't align towards the base case, it will keep on create function calls in the stack memory section.
At some point in time, the recursive function call overflows the stack memory section as it doesn't have any stopping point.
This is also called as the stack overflow in recursion.
Recursive function won't have any base case - Stack Overflow
#include<stdio.h> int fact(int n) { return n * fact(n-1); } int main() { int n; scanf("%d",&n); if(n >= 0) printf("%d\n",fact(n)); return 0; }
The above recursive function doesn't have any base case.
If the given input is 3, the recursive calls will be fact(2), fact(1), fact(0), fact(-1),.... and so on. It will never end.
This will overflows the stack memory section.
Recursive function call doesn't align towards the base case - Stack Overflow
#include<stdio.h> int fact(int n) { if(n <= 1) return 1; return n * fact(n+1); } int main() { int n; scanf("%d",&n); if(n >= 0) printf("%d\n",fact(n)); return 0; }
In the above recursive function the base case is fact(0) = 0 || fact(1) = 1.
But the function call - return n * fact(n+1).
If the given input is 5, the recursive call will be fact(6), fact(7), fact(8)....and so on. it will never end.
This will eventually overflow the stack memory section.