Dynamic Programming
In the Dynamic Programming,
1. We divide the large problem into multiple subproblems.
2. Solve the subproblem and store the result.
3. Using the subproblem result, we can build the solution for the large problem.
4. While solving the large problem, if the same subproblem occurs again, we can reuse the already stored result rather than recomputing it again. This is also called memoization.
Dynamic Programming Approaches
1. Bottom-Up approach
2. Top-Down approach
1. Bottom-Up approach
Start computing result for the subproblem. Using the subproblem result solve another subproblem and finally solve the whole problem.
Example
Let's find the nth member of a Fibonacci series.
Fibonacci(0) = 0
Fibonacci(1) = 1
Fibonacci(2) = 1 (Fibonacci(0) + Fibonacci(1))
Fibonacci(3) = 2 (Fibonacci(1) + Fibonacci(2))
We can solve the problem step by step.
1. Find Oth member
2. Find 1st member
3. Calculate the 2nd member using 0th and 1st member
4. Calculate the 3rd member using 1st and 2nd member
5. By doing this we can easily find the nth member.
Algorithm
1. set Fib[0] = 0
2. set Fib[1] = 1
3. From index 2 to n compute result using the below formula
Fib[index] = Fib[index - 1] + Fib[index - 2]
4. The final result will be stored in Fib[n].
Example
/* * Program : Nth Fibonacci using bottom-up approach * Language : C */ #include<stdio.h> int Fibonacci(int N) { //if N = 2, we need to store 3 fibonacci members(0,1,1) //if N = 3, we need to store 4 fibonacci members(0,1,1,2) //In general to compute Fib(N), we need N+1 size array. int Fib[N+1],i; //we know Fib[0] = 0, Fib[1]=1 Fib[0] = 0; Fib[1] = 1; for(i = 2; i <= N; i++) Fib[i] = Fib[i-1]+Fib[i-2]; //last index will have the result return Fib[N]; } int main() { int n; scanf("%d",&n); //if n == 0 or n == 1 the result is n if(n <= 1) printf("Fib(%d) = %d\n",n,n); else printf("Fib(%d) = %d\n",n,Fibonacci(n)); return 0; }
2.Top-Down approach
Top-Down breaks the large problem into multiple subproblems.
if the subproblem solved already just reuse the answer.
Otherwise, Solve the subproblem and store the result.
Top-Down uses memoization to avoid recomputing the same subproblem again.
Let's solve the same Fibonacci problem using the top-down approach.
Top-Down starts breaking the problem unlike bottom-up.
Like,
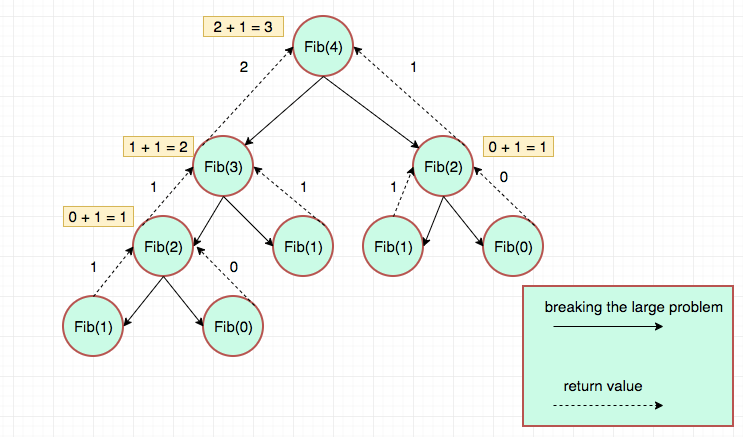
If we want to compute Fibonacci(4), the top-down approach will do the following
Fibonacci(4) -> Go and compute Fibonacci(3) and Fibonacci(2) and return the results.
Fibonacci(3) -> Go and compute Fibonacci(2) and Fibonacci(1) and return the results.
Fibonacci(2) -> Go and compute Fibonacci(1) and Fibonacci(0) and return the results.
Finally, Fibonacci(1) will return 1 and Fibonacci(0) will return 0.
Fib(4)
/ \
Fib(3) Fib(2)
/ \ / \
Fib(2) Fib(1) Fib(1) Fib(0)
/ \
Fib(1) Fib(0)
We are computing the result of Fib(2) twice.
This can be avoided using memoization.
Algorithm
Fib(n)
If n == 0 || n == 1 return n;
Otherwise, compute subproblem results recursively.
return Fib(n-1) + Fib(n-2);
Example
/* * Program : Nth Fibonacci using top-down approach * Language : C */ #include<stdio.h> int Fibonacci(int N) { if(N <= 1) return N; return Fibonacci(N-1) + Fibonacci(N-2); } int main() { int n; scanf("%d",&n); printf("Fib(%d) = %d\n",n,Fibonacci(n)); return 0; }
Visual Representation of the above algorithm
Optimizing the above program using memoization
Algorithm
1. Declare an array to store the subproblem results. i.e. result[1000]
2. Initialize the array to -1. -1 indicates that the subproblem needs to be computed.
2. Fib(N)
3. if result[N] == -1
compute and store it in result[N] using above algorithm.
5. Otherwise,
return the already computed result directly.
Example
/* * Program : Nth Fibonacci using top-down approach + memoization * Language : C */ #include<stdio.h> #define size 50 int result[size]; //initially set the result array to -1 void init_result() { int i; for(i = 0; i < size; i++) result[i] = -1; //-1 indicates that the subproblem result needs to be computed } int Fibonacci(int N) { //if the subproblem is not computed yet, //recursively compute and store the result if(result[N] == -1) { if(N <= 1) result[N] = N; else result[N] = Fibonacci(N-1) + Fibonacci(N-2); } //Otherwise, just return the result return result[N]; } int main() { int n; scanf("%d",&n); init_result(); printf("Fib(%d) = %d\n",n,Fibonacci(n)); return 0; }