Quick Sort

Quicksort is an in-place sorting algorithm which means it doesn't take an additional array to sort the data. It uses the same array to sort the elements.


Let's learn how to sort elements using the quick sorting algorithm.



Algorithm

Quicksort is a divide and conquer algorithm.

It divides the large array into smaller sub-arrays. And then quicksort recursively sort the sub-arrays.

Pivot

1. Picks an element called the "pivot".

Partition

2. Rearrange the array elements in such a way that the all values lesser than the pivot should come before the pivot and all the values greater than the pivot should come after it.

This method is called partitioning the array. At the end of the partition function, the pivot element will be placed at its sorted position.

Recursive

3. Do the above process recursively to all the sub-arrays and sort the elements.

Base Case

If the array has zero or one element, there is no need to call the partition method.

So we need to stop the recursive call when the array size is less than or equal to 1.

Pseudocode

quickSort(array, start, end)
{
    if(start < end)
    {
        pIndex = partition(arr, start, end);
        quickSort(arr, start, pIndex-1);
        quickSort(arr, pIndex+1, end);
    }
}

Let's see one by one elaborately.



Pivot

There are many ways we can choose the pivot element.

i) The first element in the array

ii) The Second element in the array

iii) The middle element in the array

iv) We can also pick the element randomly.

In our tutorial, we are going to pick the last element as the pivot element.



Partition Function

Required Details

An array          => arr[size]

Starting index => start

Ending index  => end

Initialization

Set i = start and pIndex = start

i is used to iterate the array elements.

pIndex is used to mark the final position of the pivot.


And pick arr[end] as the pivot. pivot = arr[end].

Pseudocode

pIndex = start;
pivot  = arr[end];

for(i = start; i < end - 1; i++)
{
    if (arr[i] < pivot)
    {
        swap arr[i] and arr[pIndex]
        increment pIndex by 1.
    }

    Finally, swap (arr[end], arr[pIndex]).
    return pIndex.
}



Example

Let's take an array of 5 integers.

arr[5] = {10, 25, 3, 50, 20};

start = 0.

pindex = 0.

end = 4.

pivot = 20.

Quicksort Partition 1

Diagram Explanation

No

A

B

C

1

i = 0. arr[0] = 10.
pIndex = 0.

arr[i] < pivot.
10 < 20 => True

swap(arr[i],arr[pIndex]) => swap(arr[0],arr[0])
swap(10,10).

pIndex++ => 1

2

i = 1. arr[1] = 25.
pIndex = 1.

arr[i] < pivot.
25 < 20 => False

Nil

3

i = 3. arr[3] = 3.
pIndex = 1.

arr[i] < pivot.
3 < 20 => True

swap(arr[i],arr[pIndex]) => swap(arr[3],arr[1])
swap(3,25).

pIndex++ => 2

4

i = 4. arr[4] = 50.
pIndex = 2.

arr[i] < pivot.
50 < 20 => False

Nil

5

Finally, swap(arr[pIndex], arr[end]) => swap(arr[2], arr[4]).

swap(20, 25). And return the pIndex value to the quicksort function.

Finally, pIndex = 2 and the new array will be,

10 3 20 50 25.

Now we can ensure that the all the elements before pIndex(10, 3) is lesser than the pivot(20) and all the elements after pIndex(50,25) is greater than the pivot value.

Finally, the pivot value 20 is placed in the right position (sorted).




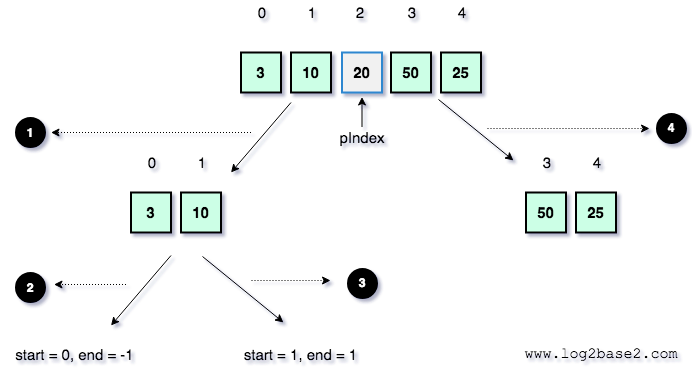
Recursive calls for the sub-arrays

Now the quicksort algorithm split the whole array into 2 small sub-arrays.


arr[0] to arr[pIndex-1]
arr[pIndex+1] to arr[end]

And executes the quickSort process on the sub-arrays. And it will happen recursively for the further sub-arrays.

In our case, pIndex = 2.

So, the next recursive calls will be


quickSort(arr, 0, 1);
quickSort(arr, 3, 4);



Recursive Call 1

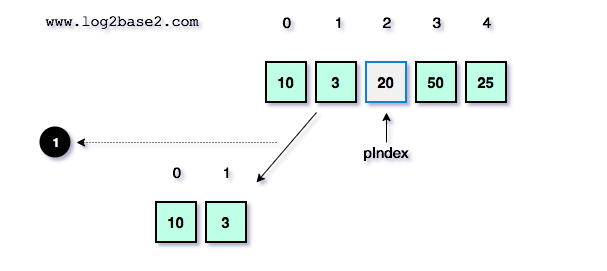
Quicksort Recursive call 1

Partition function execution for the above sub-array (10, 3).

start = 0. end = 1.

i = pIndex = 0.

pivot = 3

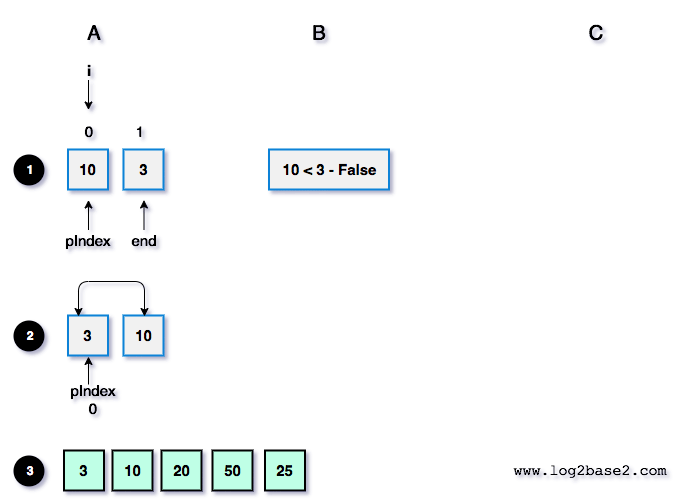
Quicksort Partition 2

Diagram Explanation

No

A

B

C

1

i = 0. arr[0] = 10.
pIndex = 0.

arr[i] < pivot.
10 < 3 => False

 Nil

2

Finally, swap(arr[pIndex], arr[end]) => swap(arr[0], arr[1]).

swap(10, 3). And return the pIndex value to the quicksort function.

3

Finally, the updated array.

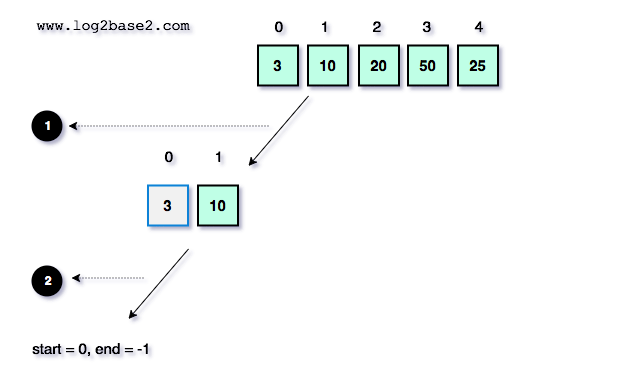
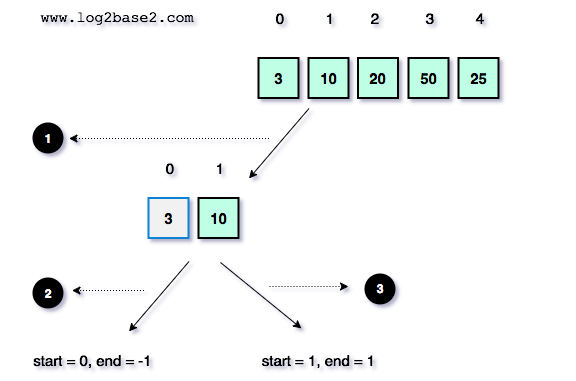
Here, pIndex value = 0.

So, the next recursive call will be


quickSort(arr, 0, -1); (Invalid index)
quickSort(arr, 1, 1); (Array has only one element)

Both are not valid. Hence the partition function will not be executed for those sub-arrays.

Recursive Call 2 and Recursive Call 3.



Recursive Call 2

Quicksort Recursive call 2


Recursive Call 3

Quicksort Recursive call 3


Recursive Call 4

Now the recursive call for the right sub-array ( index starts from 3 to 4 ) will resume,

Quicksort Recursive call 4

Partition function execution for the above sub-array (50, 25).

start = 3. end = 4.

i = pIndex = 3.

pivot = 25

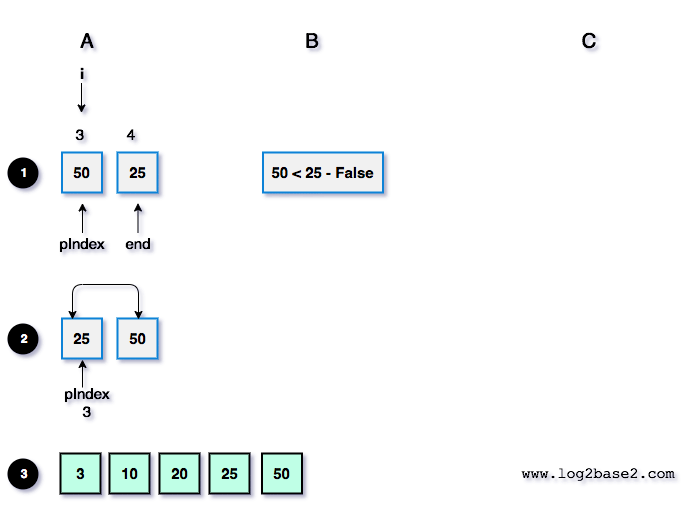
Quicksort Partition 3

Diagram Explanation

No

A

B

C

1

i = 3. arr[3] = 50.
pIndex = 3.

arr[i] < pivot.
50 < 25 => False

 Nil

2

Finally, swap(arr[pIndex], arr[end]) => swap(arr[3], arr[4]).

swap(50, 25). And return the pIndex value to the quicksort function.

3

Finally, the updated array.

Here, pIndex value = 3.

So, the next recursive call will be


quickSort(arr, 3, 2); (Invalid index)
quickSort(arr, 4, 4); (Array has only one element)

Both are not valid. Hence the partition function will not be executed for those sub-arrays.

Recursive Call 5 and Recursive Call 6.



Recursive Call 5

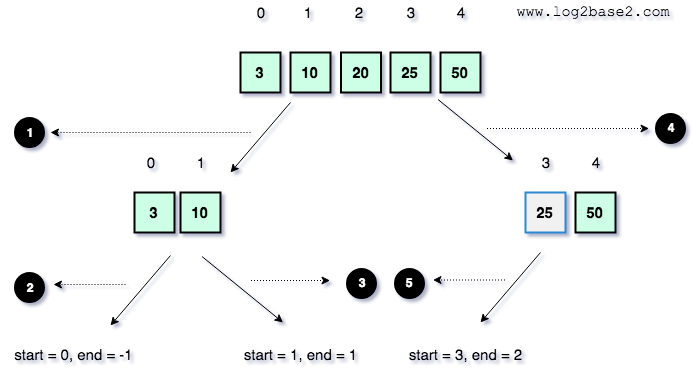
Quicksort Recursive call 5


Recursive Call 6

Quicksort Recursive call 6

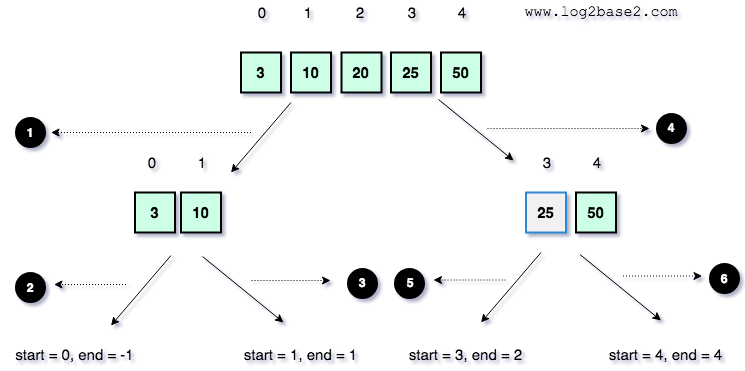
Finally, we have sorted the array. 3, 10, 20, 25, 50.



Quicksort program in c


/*
 * Program : QuickSort
 * Language : C
 */

#include<stdio.h>

void quickSort(int[], int, int);
int  partition(int[], int, int);
void swap(int*, int*);

int main()
{
    int n,i;

    printf("Enter Array Size\n");
    scanf("%d",&n);

    int arr[n];

    printf("Enter Array Elements\n");
    for(i=0;i<n;i++)
        scanf("%d",&arr[i]);

    quickSort(arr,0,n-1);

    printf("After the QuickSort\n");

    for(i=0;i<n;i++)
        printf("%d ",arr[i]);
    printf("\n");

    return 0;
}

void quickSort(int arr[], int start, int end)
{
    if(start < end)
    {
        int pIndex = partition(arr, start, end);
        quickSort(arr, start, pIndex-1);
        quickSort(arr, pIndex+1, end);
    }
}

int partition(int arr[], int start, int end)
{
    int pIndex = start;
    int pivot = arr[end];
    int i;
    for(i = start; i < end; i++)
    {
        if(arr[i] < pivot)
        {
            swap(&arr[i], &arr[pIndex]);
            pIndex++;
        }
    }
    swap(&arr[end], &arr[pIndex]);
    return pIndex;
}

void swap(int *x, int *y)
{
    int t = *x;
    *x = *y;
    *y = t;
}