Graph

A Graph is a collection of Vertices(V) and Edges(E).

Vertices also called as nodes. V is a finite set of nodes and it is a nonempty set.

Edge refers to the link between two vertices or nodes. So, E is a set of pairs of vertices.


In general,

G = (V,E).

where,

G - Graph

V - a set of nodes. Nonempty set.

E - a set of pairs of nodes. It can be an empty set.



Undirected Graph

In Undirected Graph have unordered pair of edges.

Means edge E1 (x,y) and E2 (y,x) represent the same edge.

Edge can be traversed from any direction.

Example

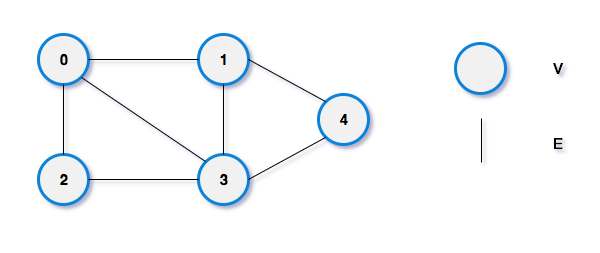
Undirected Graph

V = {0, 1, 2, 3, 4}

E = {{0,1}, {0,2}, {0,3}, {1,0},{1,3},{1,4}, {2,0},{2,3}, {3,0},{3,1},{3,2},{3,4}, {4,1},{4,3}}



Directed Graph(Digraph)

In the Directed Graph, each edge(E) will be associated with directions.

So, directed Graph have the ordered pair of edges.

Means edge E1 (x,y) and E2 (y,x) are two different edges.

Edge can only be traversed from the specified direction.

It is also called the digraph(Directed graph).

Example

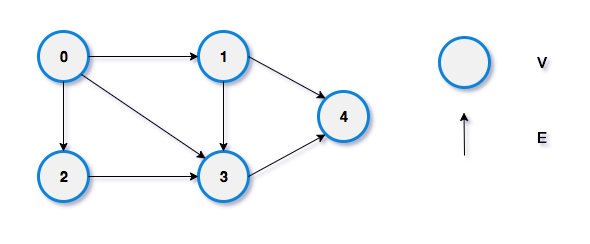
Directed Graph (Digraph)

V = {0, 1, 2, 3, 4}

E = {<0,1>, <0,2>, <0,3>, <1,3>,<1,4>,<2,3>,<3,4>}