Binary Search Tree

Binary search trees are a special kind of tree which follows the below rules,

1. Every Node should have a unique key.

2. The key in the left node should be less than the parent key.

3. The key in the right node should be greater than the parent key

4. Duplicate keys are not allowed.

Sample binary search tree with 7 nodes.

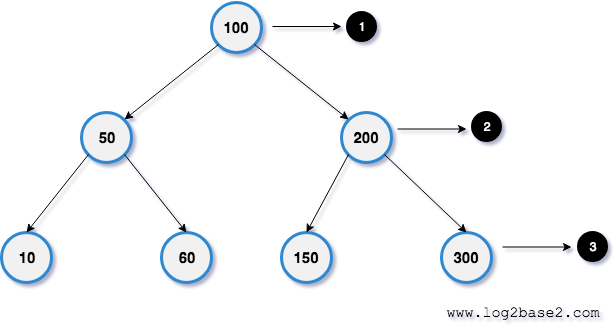
1. Root Node

The topmost node. 100 is a root node.

3. Leaf Nodes

The bottom-most nodes or the node with no reference link. 10, 60, 150, 300 are leaf nodes.

2. Internal Nodes

The nodes intermediate between root and the leaf node. 50, 200 are intermediate nodes.

Why binary search tree?

If we arrange the data based on the above rules, we can effectively manipulate them.

Example

1.

If we need to search element 10, we can do it effectively like below,

Check if the root node has the value 10. root node value = 100. 10 < 100.

Hence 10 should be present in the left subtree (right subtree must have values > 100). So we can skip entire right subtree from the searching.

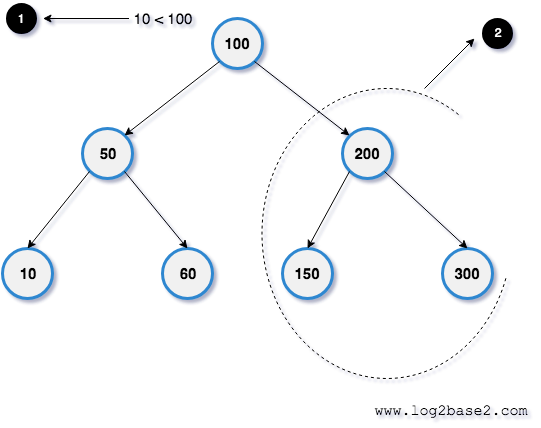
1. root's key value = 100. 10 < 100.

2. So we can skip the right subtree from the searching.

2.

Check if the left subtree's root has the value 10. Next left root value = 50. again 10 < 50.

So we can skip the right subtree from the searching as the key value less than the root.

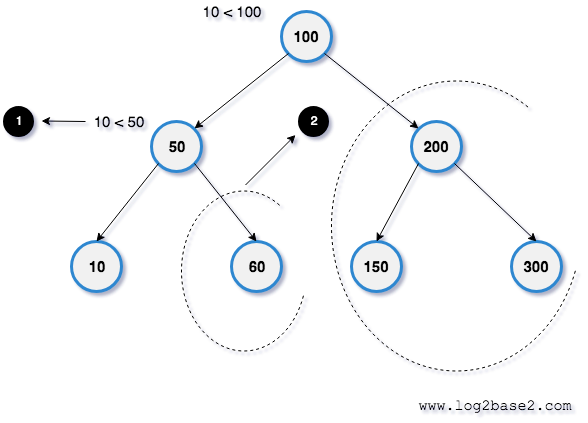
1. Left subtree's root key value = 50. 10 < 50.

2. So we can skip the right subtree from the searching.

Finally, we can find the node with value 10 in minimal search count. That's how the binary search tree effectively improves the data manipulation.

In normal array and linked list, there is no way we can skip some element from the searching as they don't follow any data arrangement rules like the binary search tree.

Binary Search Tree - Node Structure

struct node
{
    int key;
    struct node *left;
    struct node *right;
};

key - It can be any data type. char, float, double, string.

*left - Reference to the left node. It holds the memory address of the left child.

*right - Reference to the right node. It holds the memory address of the right child.

Let's create a sample BST node

struct node
{
    int key;
    struct node *left;
    struct node *right;
};

//declaring a node
struct node *root;

//allocating memory for the node
root = malloc(sizeof(struct node));

Assign values to the node

struct node
{
    int key;
    struct node *left;
    struct node *right;
};

//declaring a node
struct node *root;

//allocating memory for the node
root = malloc(sizeof(struct node));

//assigning values
root->key  =  10;
root->left =  NULL;
root->right = NULL;

Visual Representation

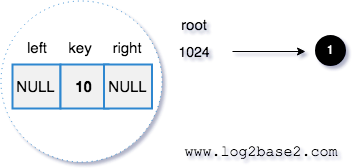
1. root node's memory address 1024. root=>data = 10. root=>left = NULL. root=>right = NULL.