Binary Number System
The computer can understand only binary number system which is also called the base 2 number system.
Binary number system = {0,1}.
Human express numbers in positional decimal format. But the computer can’t store decimal numbers directly.
The computer automatically converts the decimal number to binary format before using it.
Whatever be the data, the computer always converts it into it's only known language which is binary.
How to convert decimal numbers into binary numbers ?
Decimal to the Binary Conversion formula.
In general, decimal to any number system conversion procedure will be,
1. Take the number modulo base i.e. number % base
2. Write down the result. i.e. remainder
3. Divide the number by base i.e. number / base
4. repeat the process untill the number greater than 0. (number > 0)
Finally, rewrite all remainders in reverse order.
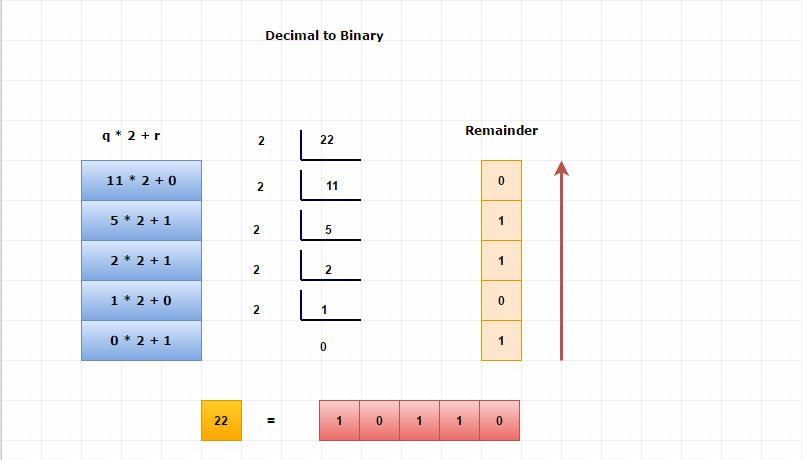
Let's convert (22)10 into Binary format,
Here, base value = 2
Pictorial Explanation
Decimal |
Binary |
|---|---|
0 |
0000 |
1 |
0001 |
2 |
0010 |
3 |
0011 |
4 |
0100 |
5 |
0101 |
6 |
0110 |
7 |
0111 |
8 |
1000 |
9 |
1001 |
Binary to Decimal Conversion
∑( ni * ( base ^ position) )
∑ denotes the summation operation.
^ denotes the power operation.
* denotes the multiplication operation.
where,
ni is each digit of a number
base
Number System |
Base Value |
|---|---|
Binary |
2 |
Decimal |
10 |
Octal |
8 |
Hexadecimal |
16 |
Position
Position varies from 0 to (number of digits – 1).
Example
For two digit numbers, the position varies from 0 to 1. For three digit numbers, the position varies from 0 to 2.
Position count starts from the right side of a number.
Example
Let's convert (10110)2 into the decimal number
where,
The position of 0 is 0.
The position of 1 is 1.
The position of 1 is 2.
The position of 0 is 3.
The Position of 1 is 4.
And the base value = 2.
(10110)2
=1*(24) + 0*(23) + 1*(22)+ 1*(21) + 0*(20)
=16+0+4+2+0
=(22)10
Pictorial Explanation
