Decimal Number System
Humans express numbers in decimal format which is also called the base 10 number system.
Decimal numbers = {0,1,2,3,4,5,6,7,8,9}
In general, base N number system will consist of numbers from 0 to N-1.
Example
Base 2 number system has numbers from 0 to 1. i.e 0 to (2 - 1).
Base 8 number system has numbers from 0 to 7. i.e 0 to (8- 1).
Positional Decimal Numbers
To represent numbers above 9, we are using positional decimal numbers.
Example
(18)10 consist of two decimal numbers which are 1 and 8.
Here,
The position of 8 is 0.
The position of 1 is 1.
Position count starts from the right side of a number.
18
= 1*(101) + 8*(100)
= 1*10+8*1
= 10+8
= (18)10
Example
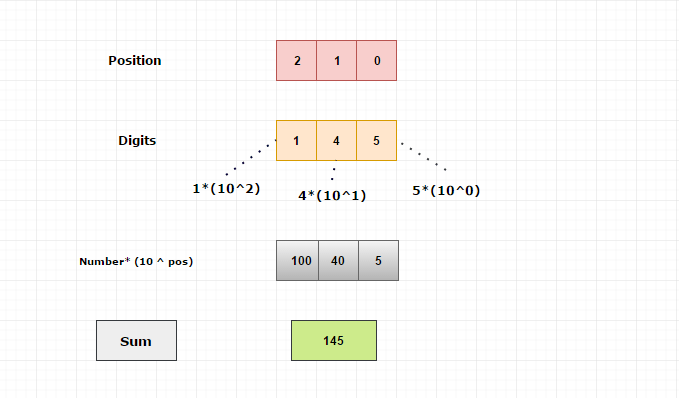
145
The position of 5 is 0.
The position of 4 is 1.
The position of 1 is 2.
(145)10
= 1*(102) + 4*(101) + 5*(100)
= 100+40+5
= (145)10
Pictorial Explanation
Real Numbers
When it comes to the real numbers or numbers with fractional parts, the position after the dot(.) will be counted as -1, -2 and so on.
Example
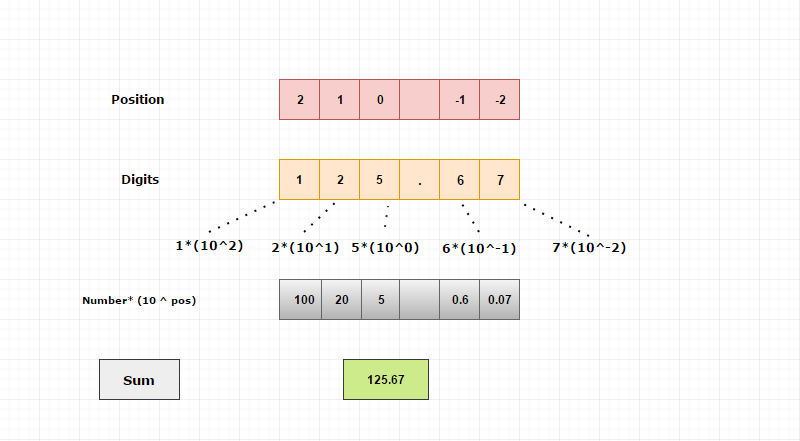
(125.67)10
The position of 6 is -1.
The position of 7 is -2.
The position of 5 is 0.
The position of 2 is 1.
The position of 1 is 2.
125.67
= 1*(102) + 2*(101) + 5*(100) + 6*(10-1) +7*(10-2)
= 100 + 20 + 5 + 0.6 + 0.07
= 125.67
Pictorial Explanation