Hexadecimal Number System
Problem Statement
In the octal system, we have grouped every 3 bits of a binary number.
But on the computer, the memory allocation always happens in multiples of 4.
Like, 1 Byte (8 bits), 4 Byte (32 bits).
How can we easily handle computer memory address?
Solution - Hexadecimal Number System
In the hexadecimal number system, we group every 4 binary bits. So that we can easily represent computer memory addresses.
Possible values that can be formed using 4 bit is 15 (1111)2.
Hexadecimal Number System = {0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F}.
It’s also called as base 16 number system.
Binary |
Decimal |
Hexadecimal |
|---|---|---|
0000 |
0 |
0 |
0001 |
1 |
1 |
0010 |
2 |
2 |
0011 |
3 |
3 |
0100 |
4 |
4 |
0101 |
5 |
5 |
0110 |
6 |
6 |
0111 |
7 |
7 |
1000 |
8 |
8 |
1001 |
9 |
9 |
1010 |
10 |
A or a |
1011 |
11 |
B or b |
1100 |
12 |
C or c |
1101 |
13 |
D or d |
1110 |
14 |
E or e |
1111 |
15 |
F or f |
The hexadecimal number system will use letters A to F to represent numbers 10 to 15.
10-A,11-B,12-C,13-D,14-E,15-F
Binary to Hexadecimal
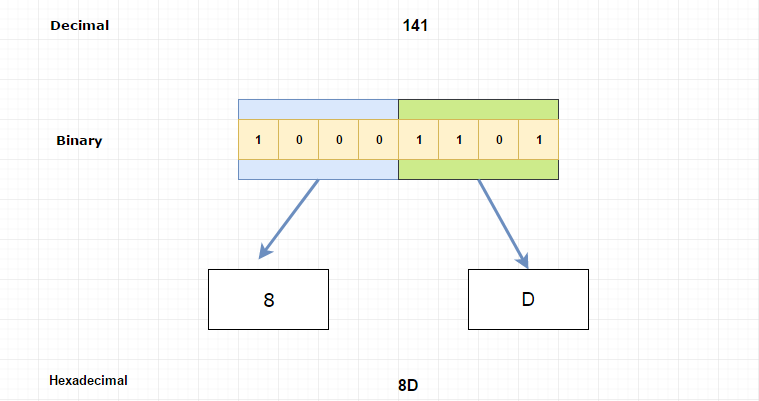
Let's convert (10001101) 2 into hexadecimal format.
Group every 4 binary bits from right to left.
Finally, combine the results.
(10001101) 2
(1000) (1101)
(1000) = (8)
(1101) = (13) ==> 13 -> D
(1000) (1101) = (8D)16
Pictorial Explanation
If the number of bits is not multiples of 4. Add zeros before the binary number to make it perfect 4-bit group.
Example
(101010) 2
Here, the number of bits is 6. By adding two zeros before the binary number, we can make it multiples of 4.
Like,(00101010) 2.
Hexadecimal to Binary
To convert the hexadecimal number into binary, we need to represent every hexadecimal digit into 4 binary bits.
Finally, combine the binary bits.
Example
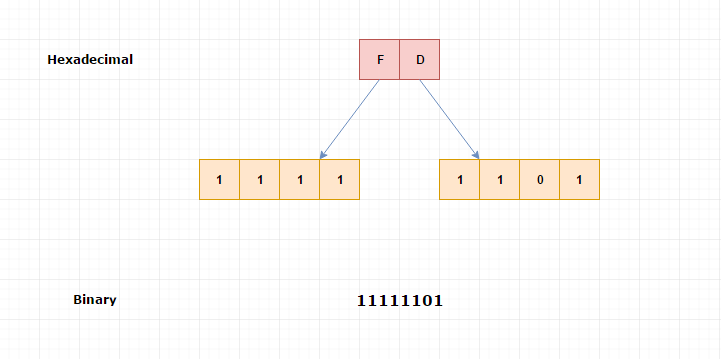
Let's convert (FD) 16 into binary numbers
(FD) 16
F= (1111)
D= (1101)
(FD) 16 = (11111101) 2
Pictorial Explanation