Octal Number System
It’s very hard to deal with binary numbers because everything will be in 0s and 1s.
To reduce the complexity, in the octal number system, we will group every 3 bits of binary in right to left direction.
The maximum value that can be formed using 3 bit is 7 (111) 2.
Octal Numbers = {0,1,2,3,4,5,6,7}
It is also called as base 8 number system.
Possible three-bit group combination will be,
Combinations |
Octal |
|---|---|
000 |
0 |
001 |
1 |
010 |
2 |
011 |
3 |
100 |
4 |
101 |
5 |
110 |
6 |
111 |
7 |
Binary to Octal
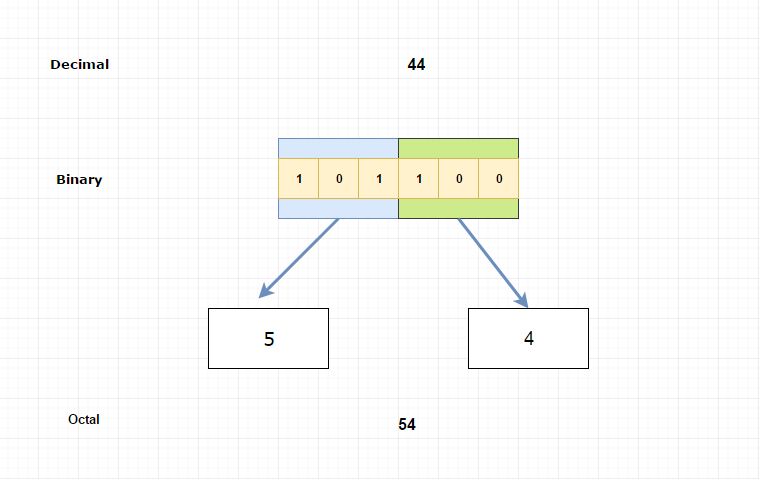
Let’s convert (101100) 2 to the octal number system.
As we discussed above, in the octal number system, we will group every 3 bits from right to left.
Example
(101) (100)
(101) = 5
(100) = 4
(101) (100) => (54) 8
Pictorial Explanation
If the number of bits is not multiples of 3, add required zeros before the binary number to make it perfect 3-bit group.
Example
(1010) 2
Here, the number of bits is 4. By adding two zeros before the binary number, we can make it multiples of 3.
Like,(001010) 2.
Octal to Binary
To convert the octal number into binary, we need to represent every digit of octal number into 3 binary bits.
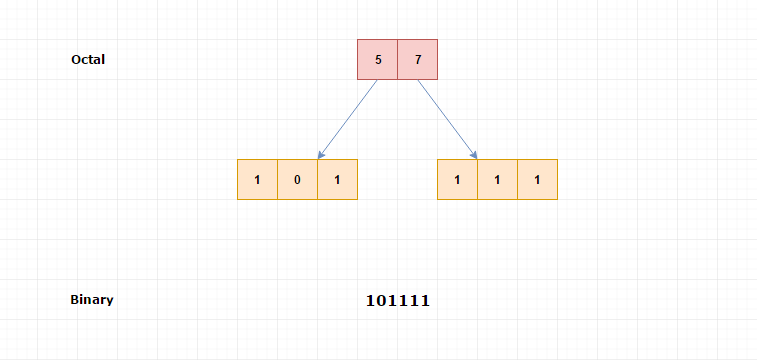
Example
(57) 8
5 = (101)
7 = (111)
(57)8 = (101111)2
Pictorial Explanation