Bitwise XOR operator
Bitwise XOR (^) operator will take two equal length binary sequence and perform bitwise XOR operation on each pair of bit sequence.
XOR operator will return 1, if both bits are different.
If bits are same, it will return 0.
The truth table,
| Ai | Bi | A i ^ Bi |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Example
Let’s take two integers say A = 5 and B = 9.
Then what will be the result of A ^ B?
Let’s represent each number in binary format.
A = (0101) 2
B= (1001) 2
Now, apply the bitwise XOR logic in each pair of corresponding bits.
Like,
Pictorial Explanation
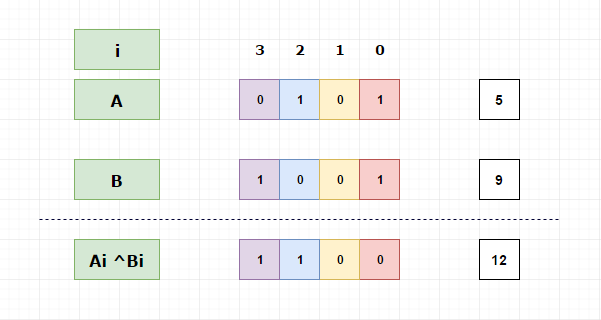
So, A ^ B will be (1100)2, which is 12.
The interesting fact here is, if we again perform XOR on the above result with 9 we will get the 5 back.
Pictorial Explanation
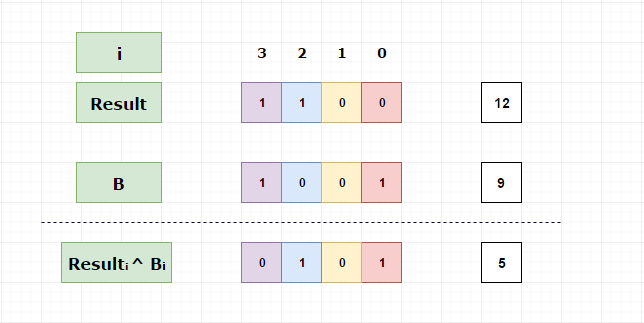
Because of this property, Bitwise XOR operator was used in cryptography initially.
XOR operator in cryptography
Assume,
5 is the value that we want to send to another person confidentially.
But if we send message 5 directly without any modification then the secrete will be a question mark.
To avoid that, the two person will share the secrete key which is only known by those two.
Let’s take secrete key as 9.
Before sending the message the sender will XOR the message with secrete key. Then the encrypted message will be sent.
After receiver got the message, he will decrypt the using the same key and get the original message.
Example
Sender,
Encryption
Secret key = 9
Message = 5
Encrypted message = 5 XOR 9 = 12
12 will be sent to the receiver rather than actual message 5.
Receiver,
Decryption
Secret key = 9
Message received = 12
Original message = 12 XOR 9 = 5
This is one of the weakest cryptography methods.